模型特点
现有的基于扩散模型的无监督异常检测方法通常遵从一个流程来重建样本,首先使用目标的正常样本来训练,然后通过加噪来重建样本。由于训练时只用了正常样本,因此只要添加的噪声足够大,就可以重建出正常样本。现有的方法通常是设置足够大的去噪步数来保证重建能力。
-
由于不同异常的图像去噪难度不均匀,设置同一个去噪步数并不一定好。由于去噪过程越长随机性更强,在重建质量更好的同时,也会导致保留原始样本的细节更少。因此本文提出了自适应去噪步骤(ADP),实现根据异常图像来自适应去噪步数。
-
在同一图像中,重建异常区域与正常区域对噪声的假设是不同的。正常区域预测的噪声是添加的噪声,也就是高斯噪声。而异常区域要预测的噪声不可避免会偏离高斯噪声,这也使得预测会更困难。本文提出了异常导向训练范式(ATP),在训练时引入合成异常图像,并推广了损失函数。ATP鼓励模型突破高斯分布的限制,提高在异常区域生成正常样本的能力。
-
为了保持细节,在推理过程中提出了空间自适应特征融合(SAFF)方案,通过融合正常区域的样本特征和异常区域的生成特征,更好地保留正常区域的细节,并减少后续对比的难度。
-
一个PCB板数据集(PCB-Bank)
准备工作
扩散过程 在前向扩散中,每次在样本 $x$ 中添加随机噪声 $\epsilon$,在 $t$ 步后的结果可以表示为
\[x_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1 - \bar\alpha_t} \epsilon\]其中 $\bar\alpha_t$ 是一个超参数,和 $t$ 相关,并且 $x_0=x$。
中间结果可视化 上式可以写成在 $t$ 步的无噪声中间结果
\[x_{t\rightarrow 0} = \frac1{\sqrt{\bar\alpha_t}}\left (x_t - \sqrt{1 - \bar\alpha_t} \epsilon_\theta(x_t,t) \right )\]其中 $\epsilon_\theta(x_t,t)$ 是预训练扩散模型预测的噪声。
生成过程 生成阶段的每一步可以写成
\[\hat{x}_{t-1} = \sqrt{\bar\alpha_{t-1}}\hat{x}_{t\rightarrow 0} + \sqrt{1 - \bar\alpha_{t-1}} \epsilon_\theta(\hat{x}_t,t)\]我们将模型预测的变量加上 $\land$ ,例如 $x_t$ 是由原图直接加噪获得,而 $\hat{x}_t$ 是由足够大的去噪步数去噪得到的。
重建误差分析
令有异常的测试样本为 $x^a$,其潜在正常样本为 $x$,这里我们有如下符号定义
\[\begin{aligned} x^a\xrightarrow{diff} x^a_T&\xrightarrow{gen} x_0 \\ x^a\xrightarrow{diff} x^a_t&\xrightarrow{gen} \hat{x}^a_0 \\ x_{t+1}^a\xrightarrow{gen} \hat{x}^a_t &\xrightarrow{vis} \hat{x}^a_{t\rightarrow 0} \\ x^a\xrightarrow{diff} x^a_t&\xrightarrow{vis} x^a_{t\rightarrow 0} \end{aligned}\]特别的有$x\xrightarrow{diff}x_t\xrightarrow{gen}x$,基本上就是遵循经过生成过程才会加上$\land$,在理想情况我们希望$\hat x^a$ 接近 $x$,此时我们就能通过 $\hat x^a$ 和 $x^a$ 来检测和定位异常。可以定义阈值$\tau$来区分正常样本和异常样本。
令异常样本$x^a$和潜在正常样本$x$之间的差异为$n$,于是有
\[x^a_t = \sqrt{\bar\alpha_t} (x_0+n) + \sqrt{1 - \bar\alpha_t} \epsilon^a\]其中$\epsilon^a$是在异常样本加的噪声。定义从$t$步开始的生成过程为$g_t$,于是可以得到误差
\[\begin{aligned} \hat{x}^a-x&=g_t(x^a_t) - g_t(x_t) \\ &=g_t(\sqrt{\bar\alpha_t} x_0 + \sqrt{1 - \bar\alpha_t} \epsilon^a+\sqrt{\bar\alpha_t} n)-g_t(\sqrt{\bar\alpha_t} x_0 + \sqrt{1 - \bar\alpha_t} \epsilon) \\ &\overset{\propto}\sim\sqrt{1 - \bar\alpha_t}(\epsilon^a-\epsilon)+\sqrt{\bar\alpha_t} n \end{aligned}\]其中$\overset{\propto}\sim$为估计正比于,在$g_t$平滑假设下可以得出。然后就是想办法减少这个损失。
训练阶段
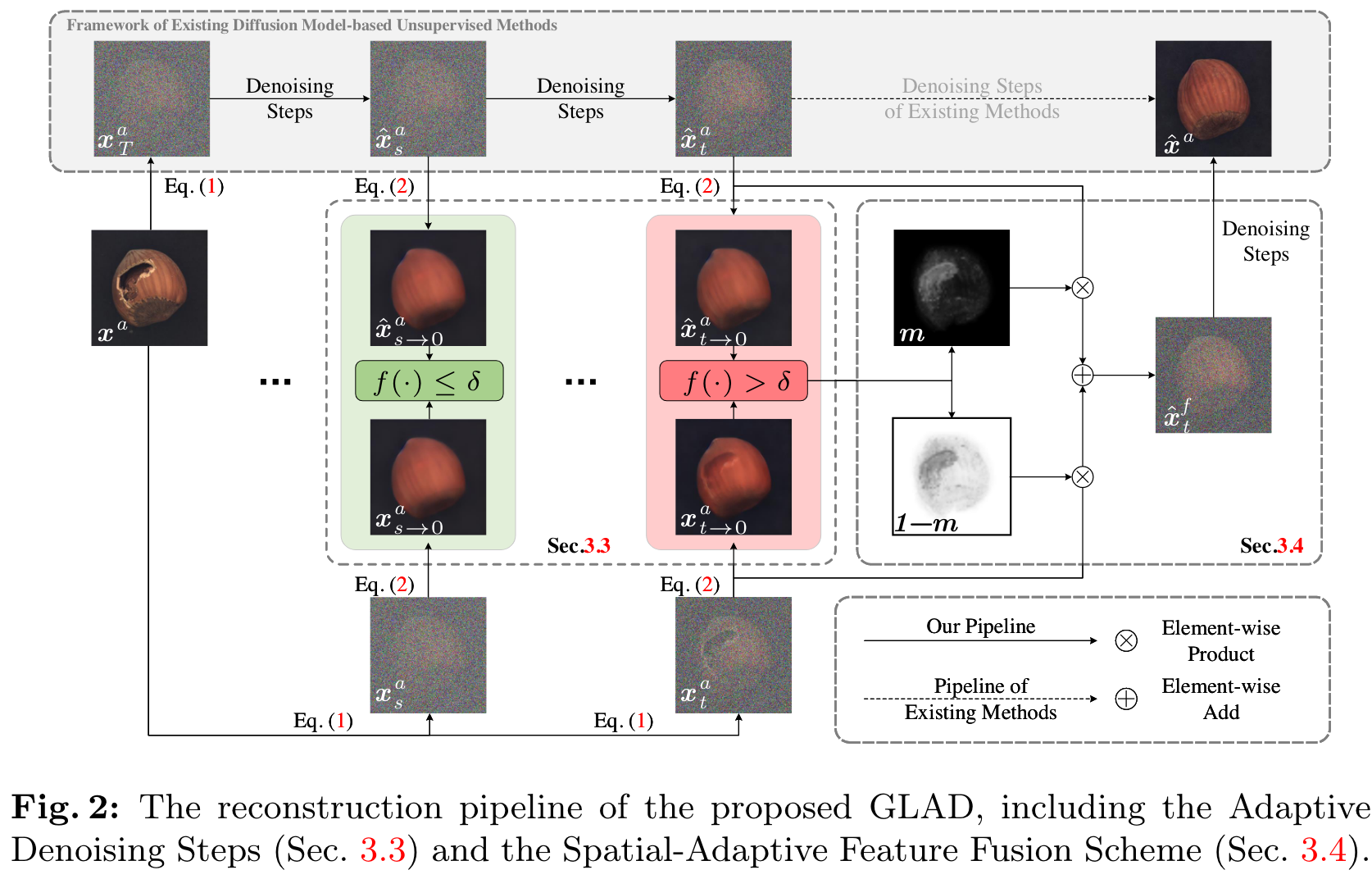
自适应去噪步数(ADP)
在前面的误差分析中,如果忽略$\epsilon^a$和$\epsilon$之间的差异,还剩下$\sqrt{\bar a_t}n$。对于比较大的$n$,需要更小的$\sqrt{\bar a_t}$,也就需要更大的$t$。可以通过判断$x^a_t$和$\hat x^a_t$,这里的$\hat x^a_t$由$x^a_T$生成,认为最终生成的是正常样本,$x^a_t$为直接加噪获得。考虑到这两个特征都带有噪声,最终比较的是无噪声的版本$x^a_{t\rightarrow0}$和$\hat x^a_{t\rightarrow0}$。通过阈值$\delta$来判断起始去噪步数,看fig.2的红绿框。找到$t$后选择从$t+n$步开始,为了保持一些冗余。
空间自适应特征融合(SAFF)
然而并不用对整个图像设定去噪步骤$(t+n)$,可以只对异常区域设定更大的去噪步骤。对于正常区域还是设定去噪步骤$t$,对潜在的异常区域设定较大的去噪步骤。在ADP中已经从步骤$T$执行了去噪到$t$获得了$\hat x_t^a$,可以在此过程中重用。具体的,可以推导出一个掩膜$m$,表示像素成为异常的一部分的可能性,然后可以将两个特征结合得到
\[\hat x_a^f =m\cdot \hat x_t^a + (1-m)\cdot x_t^a\]由于存在噪声偏差问题,我们用无噪声版本加上相同的噪声$\epsilon$得到一致噪声
\[\begin{aligned} \hat x^f_t &= \sqrt{\bar\alpha_t} \hat x^f_{t\rightarrow 0} + \sqrt{1 - \bar\alpha_t} \epsilon \\ &=\sqrt{\bar\alpha_t}(m\cdot \hat x^a_{t\rightarrow 0} + (1-m)\cdot x^a_{t\rightarrow 0}) + \sqrt{1 - \bar\alpha_t} \epsilon \end{aligned}\]异常导向训练范式(ATP)
在前两节后还有一个问题要解决,让重建差异减少实质是让下式越接近零
\[\hat x^a-x\overset{\propto}\sim\sqrt{1 - \bar\alpha_t}(\epsilon^a-\epsilon)+\sqrt{\bar\alpha_t} n\rightarrow 0\]这里$\bar\alpha_t,\epsilon,n$都是事先设定或者能中途计算的,只有$\epsilon^a$需要模型来估计,将上式重写可以得到
\[\epsilon^a\rightarrow\epsilon-\frac{\sqrt{\bar\alpha_t}}{\sqrt{1 - \bar\alpha_t}}n\]其中$\epsilon\sim\mathcal{N}(0,1)$遵循了高斯分布,为了在训练时让扩散模型突破高斯分布的限制,可以用以下优化目标
\[\begin{aligned} L_{ATP} &= \mathbb{E}_{(x^a,x)\sim p_{data},\epsilon\sim\mathcal{N}(0,1),t}\left[\left\|\epsilon^a - \left(\epsilon - \frac{\sqrt{\bar\alpha_t}}{\sqrt{1 - \bar\alpha_t}}n\right)\right\|_2\right] \\ &= \mathbb{E}_{(x^a,x)\sim p_{data},\epsilon\sim\mathcal{N}(0,1),t}\left[\left\|\epsilon_\theta(x^a_t,t) - \left(\epsilon - \frac{\sqrt{\bar\alpha_t}}{\sqrt{1 - \bar\alpha_t}}(x^a-x)\right)\right\|_2\right] \end{aligned}\]可以看出,上式要求正常样本和异常样本的配对,这里借鉴了MamSag,使用了合成异常数据。
测试阶段
参考AprilGAN,使用预训练模型DINO对测试图像$x_t$和重建图像$x_r$提取特征得到多层特征$F_t$和$F_r$。$l$层的异常图$M_l\in\mathbb{R}^{u\times v}$由$l$层的特征$F^l_t\in\mathbb{R}^{c\times u\times v}$和$F^l_r\in\mathbb{R}^{c\times u\times v}$计算余弦相似度获得
\[M_l(F_t^l,F_r^l)(i,j)=\min_{m,n}(1 - <F_t^{l}(i,j),F_r^{l}(m,n)>)\]其中$(i,j)$是坐标,最后对$l$层求和得到异常图
\[M=\sum_{l} M_l(F_t^l,F_r^l)\]选择最高的$K$个值的均值作为image-level的异常分数。